パーセプトロン

大規模言語モデルの仕組みを理解したいのですが、そもそもDeep Learningの仕組みを理解しないといけないらしい。ということで「ゼロつく」こと「ゼロから作るDeep Learning」の第1作目から見ていきます。

Deep Learning（= ニューラルネットワーク）は、パーセプトロンが起源になってるとのこと。パーセプトロンって何でしょう？？

まずは図であらわすと、コレです。

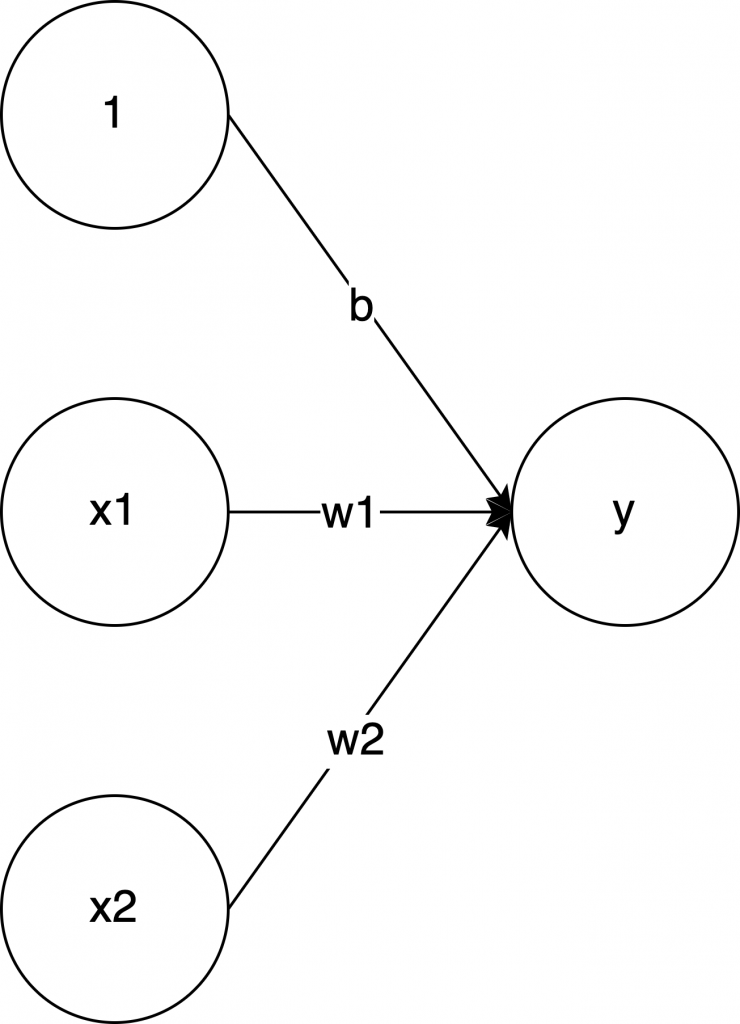
意味わからないですね。数式であらわすとコレです。

\[
y = \begin{cases}
0 & (w_1 x_1 + w_2 x_2 \leq b) \\
1 & (w_1 x_1 + w_2 x_2 > b)
\end{cases}
\]

パッと見た感じ、もっと意味わからないです。数式が出てくると、無視するか、一次方程式とか読めそうだったら頑張ってみる、のどっちかだと思います。自分はこの式は頑張って読みました。

\( x_1 \) と \( x_2 \)という2つの入力値があって、それぞれに \( w_1 \) と \( w_2 \) を掛けた結果が、\( b \) より多ければ \( 1 \) 、それ以外は \( 0 \) を出力する、ということのようです。\( w_1 \) と \( w_2 \) を重み、\( b \) をバイアス（偏り）と言います。

そういうアルゴリズムのことを、パーセプトロン、と言います。

このパーセプトロンを使うと、AND回路（論理積）とか、OR回路（論理和）とかを表現できます。エンジニアにとっては、コードにするとわかりやすいです。AND回路をコードにすると以下になります。ゼロつくと同じPythonで書きます。

def AND(x1, x2):
    w1, w2, b = 0.5, 0.5, 0.7
    tmp = x1*w1 + x2*w2
    if tmp <= b:
        return 0
    elif tmp > b:
        return 1

シンプルですね。0.5 と 0.7 という数値は条件を満たせればどんな値でも良いのです。この関数は AND(0, 0) の場合 0 を返し、AND(1, 1) の場合は 1 を返したりと、AND回路になっています。この調子でパーセプトロンを使うと、AND, OR, NAND（否定論理積） は作れます。

でも一つのパーセプトロンだと、XOR（排他的論理和） は作れない…。

XOR の入力と出力のパターンは以下です。

1 XOR 1 = 0
0 XOR 1 = 1
1 XOR 0 = 1
0 XOR 0 = 0

\(x_1\) と \(x_2\) が違う場合だけ \( 1 \) になるやつです。これは先ほどの w1, w2 などの数値を調整してもできない。（なぜなら非線形だから、とのことですが省略…）

とにかく一つだけのパーセプトロンだと作れないので、複数組み合わせて作ります。コードです。

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

NAND関数, OR関数の実装は省略してますが、ここで重要なのは、パーセプトロンを重ねることで、単体では表現できなかった XOR を作ることができた、という点です。

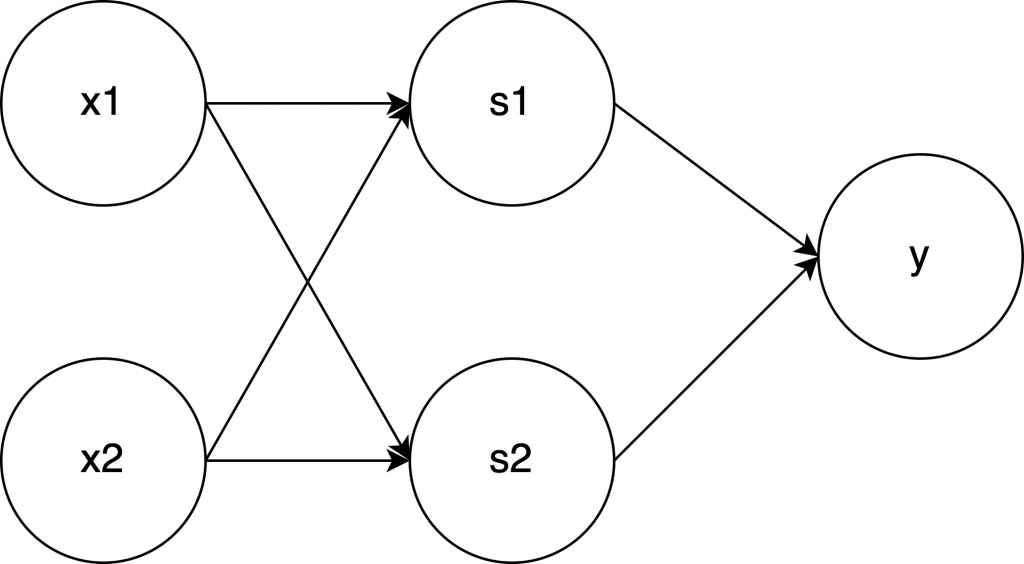
この層を重ねているのが重要です。\( x_1 \) と \( x_2 \) のところが一つの層で、\( s_1 \) と \( s_2 \) も層で、という具合です。これがニューラルネットワークに似ていて、その起源と呼ばれる所以とのことです。