ニューラルネットワーク – AIに怯える日々から脱却するためのブログ

前回のお話ではニューラルネットワークの起源と言われるパーセプトロンについて見ていきました。

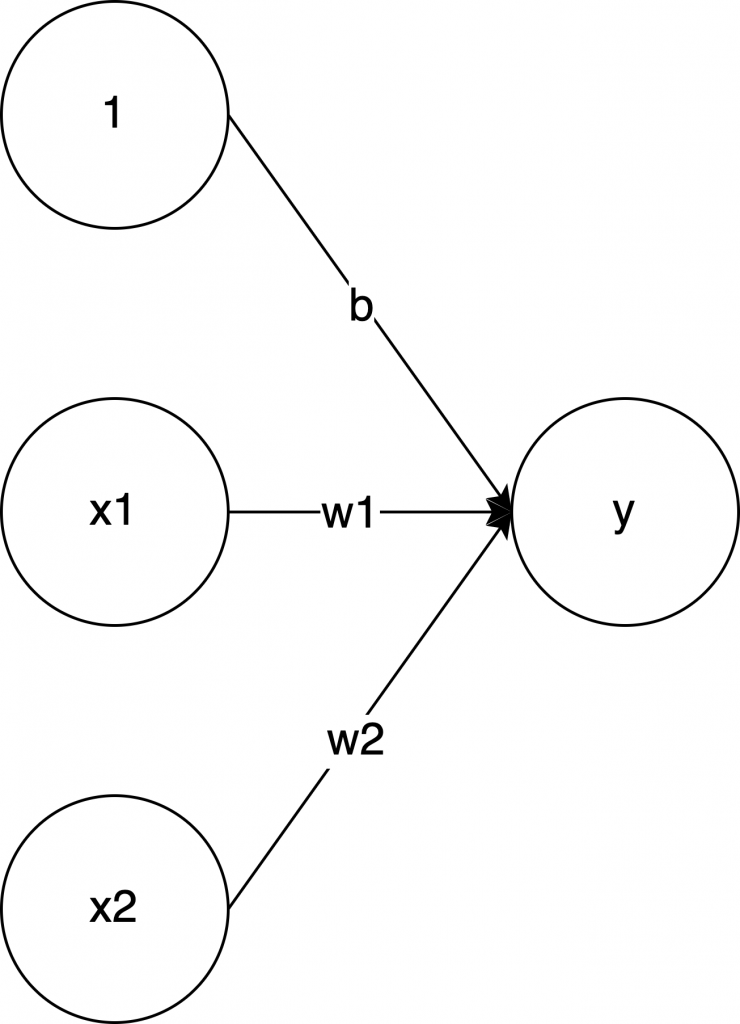
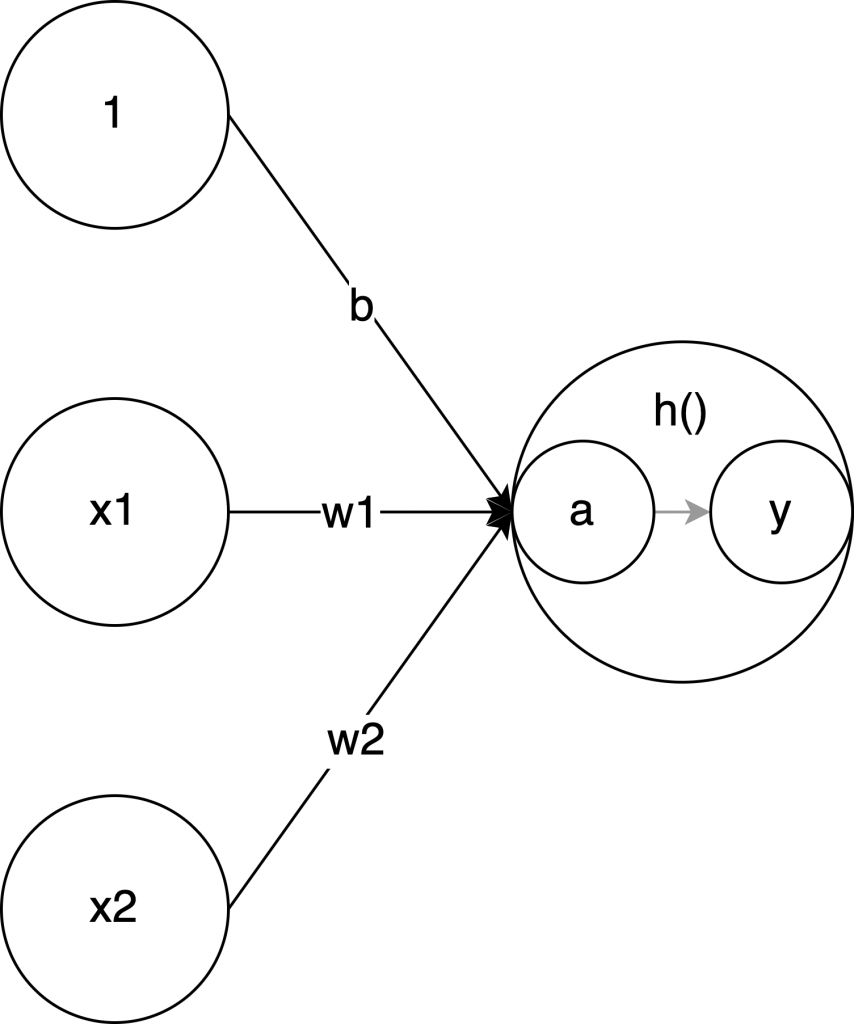
ざっくりおさらいすると、入力値が2つあって、それを \( x_1 \) と \( x_2 \) とすると、それぞれに重み \( w_1 \) と \( w_2 \) を掛けて、さらに \( b \) を足した結果が \( 0 \) より大きい場合は \( 1 \) を出力して、以下の場合は \( 0 \) を出力する、というアルゴリズムでした。（ざっくりといいながら、全部説明してる）

このアルゴリズムを2つ重ねることによって、XOR（排他的論理和）が作れます。

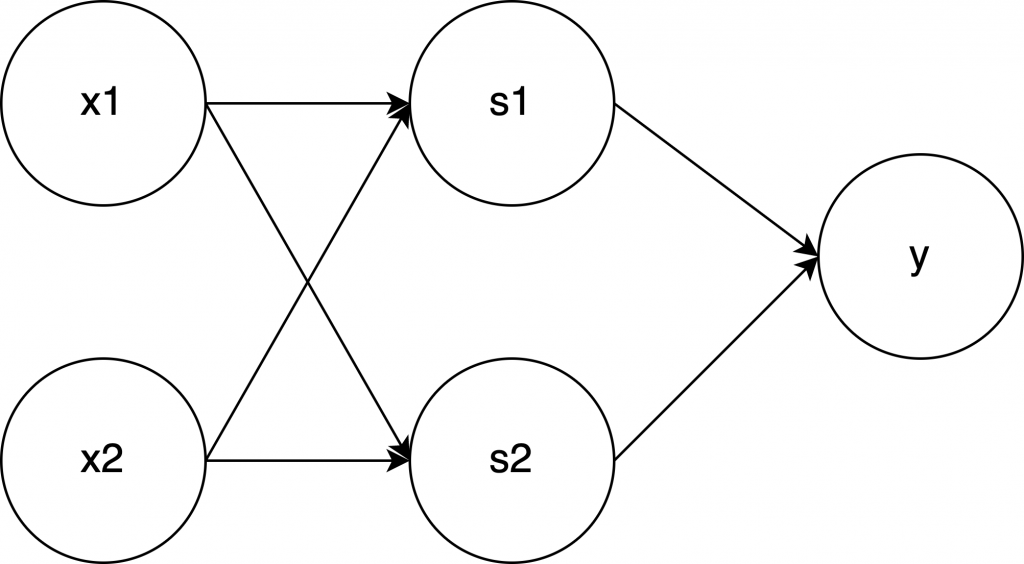
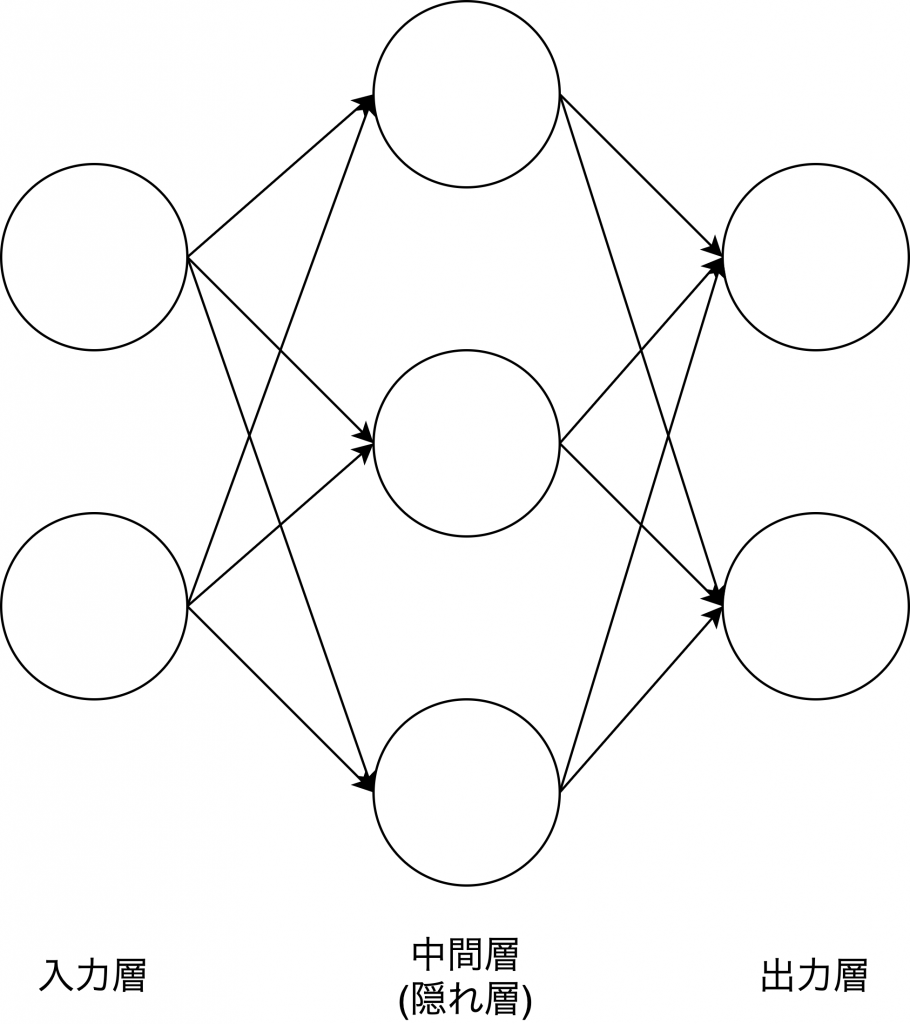
ニューラルネットワークも同じように、入力と出力をつなげたネットワークのようです。以下図のようにです。図の ○ のことをニューロンとかノードとか言ったりします。ニューロンのネットワークだから、ニューラルネットワークなんです。

以下記事がわかりやすいです。

https://qiita.com/begaborn/items/3fb064215d7f6e6cce96

縦に並んだ ○ を一つの”層”としていて、それぞれ入力層・中間層・出力層と呼ばれます。パーセプトロンの XOR と同じになってますね。中間層は1層だけじゃない場合もあります。

行列の計算

ここから数学の話なんですが、正直、最初は読み流してました。でも記事を書くにあたりDeep learningのゼロつくを読み返してるうちに、この基礎のところがとても重要なんだと思うようになりました。

のでしっかり書きたいと思います。

以下の図のニューラルネットワークの計算をしたいと思います。

実装するニューラルネットワーク

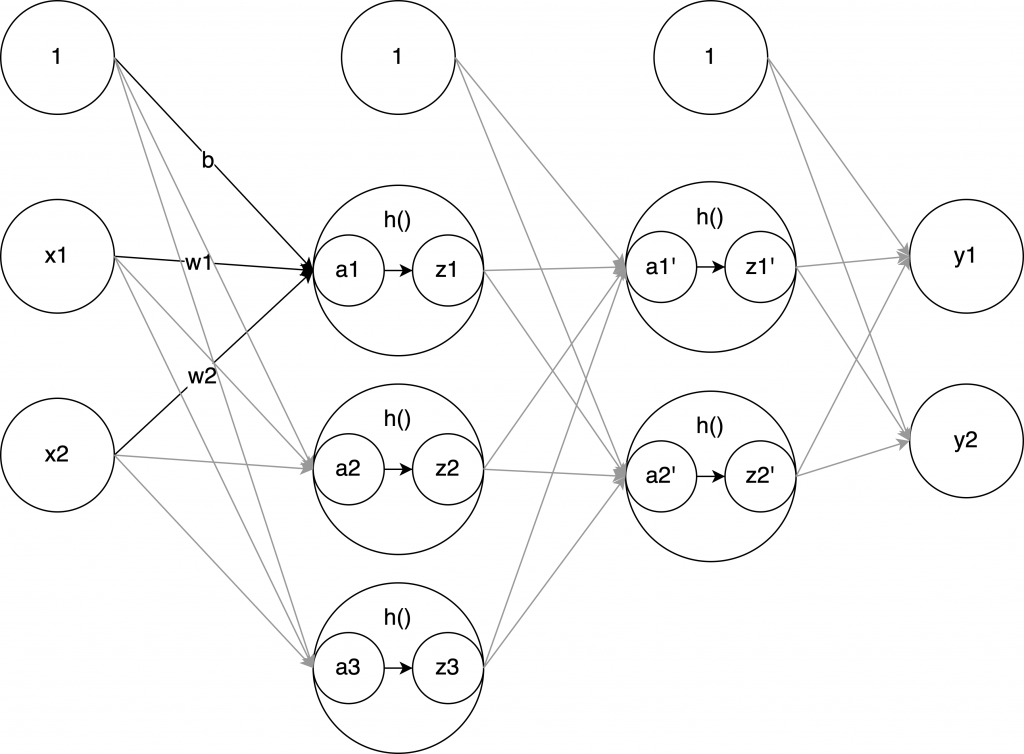
入力層

\( x_1 \) , \( x_2 \)

中間層一つ目

\( a_1 \) , \( a_2 \) , \( a_3 \)

中間層二つ目

\( a_1′ \) , \( a_2′ \)

出力層

\( y_1 \) , \( y_2 \)

入力が2つで、中間層一つ目の3つのパラメータ（とバイアス）、中間層二つ目の2つのパラメータ（とバイアス）を経て、最終的に出力が2つになっています。

パーセプトロンの XOR の例だと入力が2つ、中間層のパラメータが2つ、出力が1つ、でしたよね。それが増えただけです。増えただけですが、中間層で活性化関数 \( h() \) というやつが登場しています。

活性化関数

図の \( h() \) となっているところです。\( a_1 \) を入力にして \( z_1 \) を出力している関数です。

なぜ中間層では、そのまま次のニューロンに値を渡さず、活性化関数で値を変換する必要があるのでしょうか？

→ それは非線形にしたいからです。活性化関数はいくつか種類がありますが、どれも非線形。

非線形ってなんでしょうか…？

→ 線形は一時方程式のようにグラフにしたときに直線で、非線形は曲線だったりギザギザだったりします。非線形の関数を挟むことで、ネットワークにして層を重ねる意味が出てきます。逆に、一時方程式（線形）の関数を活性化関数として使った場合を考えてみます。例えば \( h(x) = cx \) というの場合、3層重ねたら、それは \( y(x) = h(h(h(x))) \) が最終的な出力になります。これは結局、 \( y(x) = c \times c \times c \times x \) と同じ意味で 1層で表現できてしまい、ネットワークにする意味がなくなってしまいます。（ゼロつくで説明されている例です）

活性化関数について見ていきます。

ステップ関数

パーセプトロンでも実はこの関数を使用してました。「0より大きいなら1、0未満であれば0を出力する」という部分がそれです。渡ってきた入力をそのまま流さず、ちょっと値を変えて出力します。それが活性化関数です。

ステップ関数に渡す入力値と出力値の関係をグラフにすると以下になります。

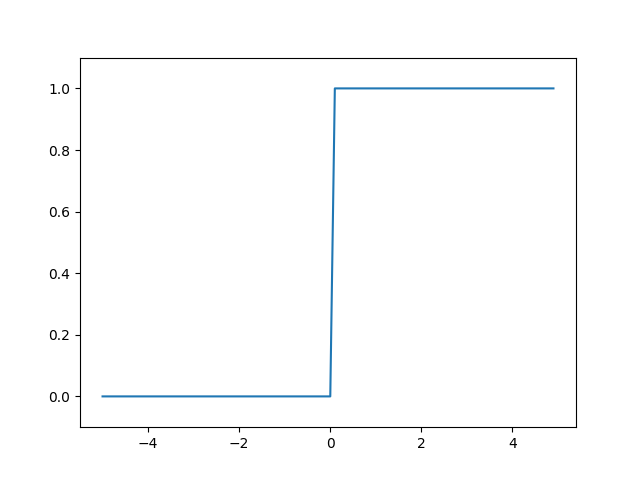
シンプルです！横軸が入力値です。それが 0 より小さければ 0, 大きければ 1 になっています。

シグモイド関数

大規模言語モデル入門でも出てくるよ！

ステップ関数を滑らかにしました。yの値が0〜1の間でキレイな曲線を描いています。

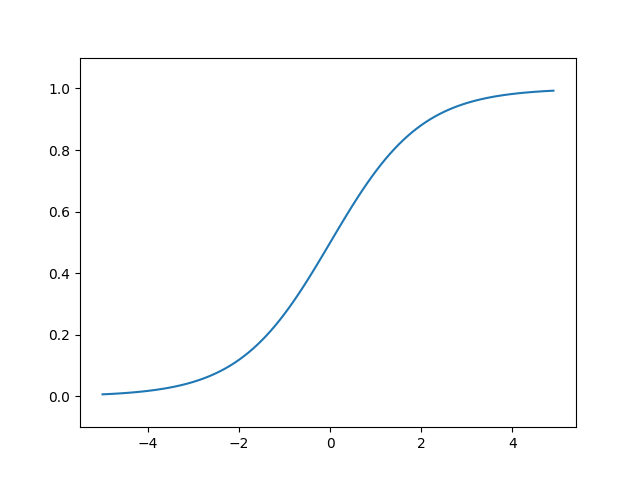
一応、実装に関わるので数式も載せておきます。（数式を見てもピンとこないのに、コードを見るとなんとなくわかった気がするのはなぜでしょうか）

\[
h(x) = \frac{1}{1 + e^{-x}}
\]

うん、 \( e^{-x} \) がわからない。ChatGPT！

ネイピア数 e を底とする指数関数の減衰型（下り坂）を表します。以下にわかりやすく解説します。

⸻

そもそも「e」ってなに？
• 約 2.718 の無理数。
• \( e^x \) は「増え方が自分自身に比例する関数」。
• つまり、増えれば増えるほど、もっと増える（株価がバブル状態になる感じ）。
• 対して e^{-x} は、増えれば増えるほど、どんどん減る。

⸻

\( e^{-x} \) の直感的な意味
• 「e の x 乗の逆数」です。
\( e^{-x} = \frac{1}{e^x} \)
• x が大きくなるほど、分母が大きくなるので値はどんどん小さくなる。
• x = 0 のとき： \( e^0 = 1 \)
• x = 1 のとき： \( e^{-1} \approx 0.3679 \)
• x = 5 のとき： \( e^{-5} \approx 0.0067 \)

…OK。ちなみに \( e \) は \( exp \) と書いたりもするそうです。

たしかにこの式だと、グラフの形になりそうですね！

ReLU関数

ステップ関数のパワーアップ版でしょうか。（語彙力）

\( x \) が0より大きいときは斜めになっています。

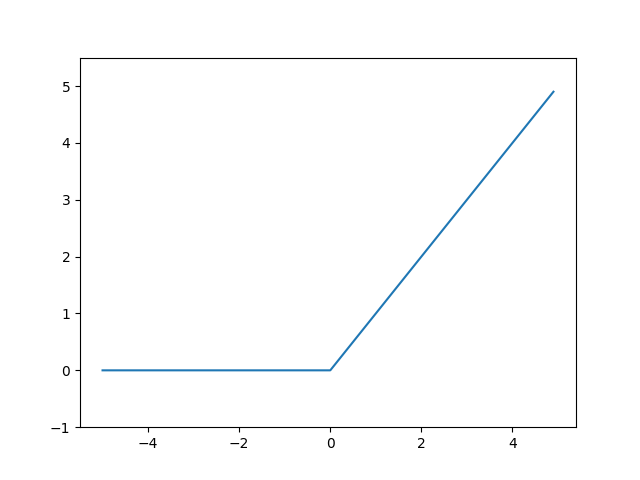
式です。

\[
h(x) =
\begin{cases}
x & (x > 0) \\
0 & (x \leq 0)
\end{cases}
\]

いつか使う時がくるかもしれません。

行列の掛け算と足し算

ニューラルネットワークの図を計算するのに、行列はとっても便利です。実装する図をもう一度載せます。

まず、入力層の値を行列で表してみましょう。

\[
\begin{bmatrix}
1.0 & 0.5
\end{bmatrix}
\]

二つの値があります。これは、1行（横）、2列（縦）です。エクセルに慣れてればなんてことないです。\( x_1 = 1.0 \) で \( x_2 = 0.5 \) ということです。

次に中間層の値を出したいのですが、入力層のそれぞれの値に重み \( w \) をかけてます。そこで行列の積の登場です。掛け算する行列 \( w \) は以下になります。

\[
\begin{bmatrix}
0.1 & 0.3 & 0.5 \\
0.2 & 0.4 & 0.6
\end{bmatrix}
\]

\( a_1 \) は \( x_1 = 1.0 \) と \( x_2 = 0.5 \) に、それぞれ、\( w \) の1列目である \( 0.1 \) と \( 0.2 \) を掛けた結果を足しています。この計算自体が行列の積の計算そのものなのです。残りの \( a_2 \), \( a_3 \) も同様に計算します。図に照らし合わせると、\( w1 \) が \( 0.1 \), \( w2 \) は \( 0.3 \) にあたります。

ただし、あと少しです。 \( a_1, a_2, a_3 \) は \( b \) を足す必要があります。ここでは行列の足し算を行います。足し算はすべての行列のそれぞれ同じ位置の要素同士を足すだけです。ここでの \( b \) をスカラー値といったりします。\( b \) は以下です。

\[
\begin{bmatrix}
0.1 & 0.2 & 0.3
\end{bmatrix}
\]

なので計算結果は以下になります。

\[
\begin{bmatrix}
0.2 & 0.5 & 0.8
\end{bmatrix}
\] \[
+ \begin{bmatrix}
0.1 & 0.2 & 0.3
\end{bmatrix}
\] \[
= \begin{bmatrix}
0.3 & 0.7 & 1.1
\end{bmatrix}
\]

実装

先ほど解説した行列の計算部分をPythonで書くと以下になります。

a1 = np.dot(x, W1) + b1

すごすぎる！そりゃあ、PythonがAIでよく使われるわけです。。。 x とか W1 は、配列になります。行列を配列で表現しています。以下にコード全文載せます。


import numpy as np

def init_network():
    network = {}
    network['W1'] = np.array([
        [0.1, 0.3, 0.5], 
        [0.2, 0.4, 0.6],
    ])
    network['b1'] = np.array(
        [0.1, 0.2, 0.3]
    )
    network['W2'] = np.array([
        [0.1, 0.4], 
        [0.2, 0.5], 
        [0.3, 0.6],
    ])
    network['b2'] = np.array(
        [0.1, 0.2]
    )
    network['W3'] = np.array([
        [0.1, 0.3], 
        [0.2, 0.4],
    ])
    network['b3'] = np.array(
        [0.1, 0.2]
    )
    return network

def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def identity_function(x):
    return x

def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y

network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y) # [0.31682708 0.69627909]

identity_function() ですが、出力層の活性化関数は別の関数を使います。ここでは値をそのまま出しているだけです。説明します。

出力層で使う活性化関数

そもそもですが、ニューラルネットワークは、

分類問題

→ クラス分け。画像認識で「人」と分類するなど

回帰問題

→ 今までのデータから予測して出そうな答えを求める（値を出す）

に分類される問題を解くものです！（今更・・・）

なので出力層で出てきた値は上記の問題を解くための値にする必要があります。そのために使用する関数は、以下などがあります。

恒等関数: （回帰問題）
シグモイド関数:（2クラス分類問題）
ソフトマックス関数:（多クラス分類問題）

などを使います。 identity_function() は恒等関数になります。

ソフトマックス関数

出力層で使用する関数のうち、「ソフトマックス関数」について説明します。

大規模言語モデル入門でも出てくるよ！

まあ、これだけではないですが、大規模言語モデル入門では、大体ゼロつくの知識は全部知っている前提でさらっと出てきます。。。

ソフトマックス関数の役割をざっくりいうと、複数の数値を「確率」に変換する関数です。

AIといえば、ChatGPTが出る前までは、分類問題のイメージが強かったです。ある画像をAIで計算して、犬なのか、猫なのか、などの分類をしてくれるものです。それに使います。

例えば、ある数字の手書き画像（行列に変換したもの）をニューラルネットワークで計算して、出力層を 0 〜 9 の 10個にする場合、”0″ の確率が 0.01, “1” の確率が 0.9 … “9” の確率が 0.0001 などの結果が出ると、この画像は “1” の可能性が高いなぁということがわかる訳です。

数式です。

\[
\text{softmax}(x_i) = \frac{e^{x_i}}{\sum_{j} e^{x_j}}
\]

出ました… \( \sum \) 。頑張って読み解いてみます。

\( \text{softmax}(x_i) \) は、出力層で出力される各ニューロンの値です。”0″ が出る確率、”1″が出る確率、などです。確率なので、全体のうちどのくらいの割合かを計算すればいいので、例えば、”0″がでる確率を求めたければ、その値を全部の値の合計で割ればいいですよね。それが \( \frac{e^{x_i}}{\sum_{j} e^{x_j}} \) の部分です。

なぜ \( e \) の \( x_i \) 乗してるのか？ChatGPT！

指数関数の「差を強調する」性質

たとえばスコアが少し違うだけでも、指数関数に通すとその差が大きくなる：
• 例：元のスコア → [2, 1, 0]
• \( e^x \) を通すと → [7.39, 2.72, 1.00]

これにより、最も高いスコアが目立つようになる。
→ ソフトマックスが「一番それっぽいクラス」に高い確率をつけやすくなる。
⸻

微分がキレイで計算しやすい

機械学習では勾配（微分）を使って学習します。
\( e^x \) は微分しても変わらない \( (\frac{d}{dx}e^x = e^x) \)ため、学習時の計算がシンプルになります。
⸻

0〜1の確率に自然と変換できる

指数関数を使って各値を変換し、全体の合計で割ると必ず合計が1になる。
→ これは確率として非常に自然な性質。

…OK。とにかく確率を求めるために使う関数なんだ…！

最後に、ゼロつくに載っていた図がわかりやすいので引用させていただきます。\( σ() \) は出力層の活性化関数であることを示しています（中間層の活性化関数は \( h() \) でした）

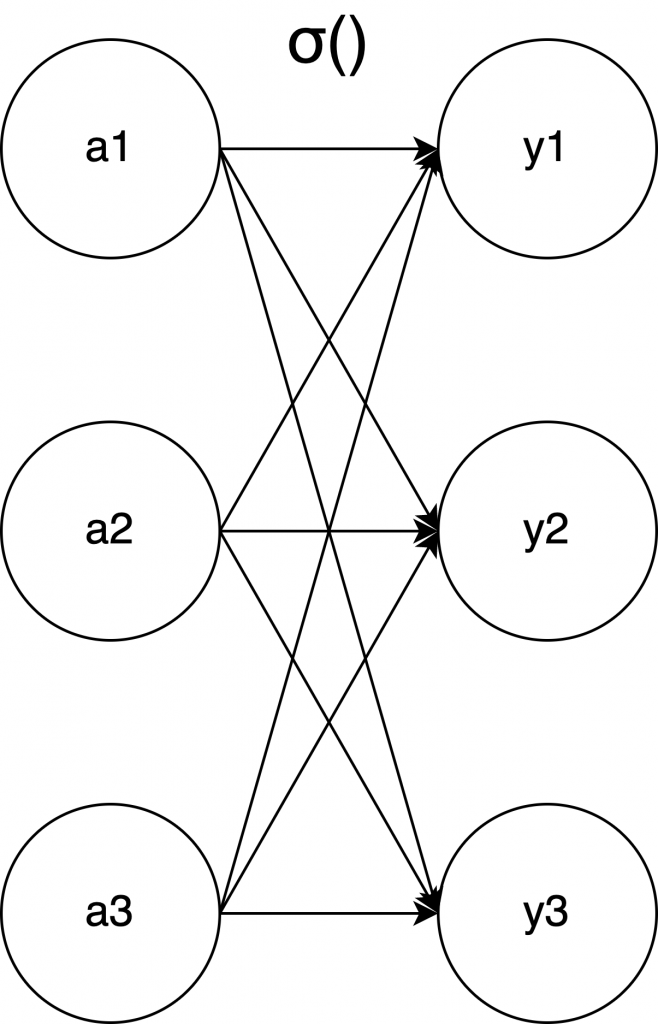
引用: 斎藤康毅著. 『ゼロから作るDeep Learning』. オライリー・ジャパン社. 2016, 67ページ

まとめ

ニューラルネットワークの概要と行列の計算、実装と見ていきました。

ところで・・・いったい何をやってるのでしょうか？

これが大規模言語モデルにどう繋がるんでしょうか。

挫折した大規模言語モデル入門の最初の方で、どうやら単語を行列の値に変換して計算してそう、というのはわかりました。「犬」のような単語を、 \( [1.0, 0.2, 0.5] \) などに変換して計算する訳です。それがどうしてあんなChatGPTみたいなやつになるのか、不思議で仕方ありませんが、とにかく最初の一歩は踏み出しました。

今日は長くなったのでここまでです。ありがとうございました。